Глава 3. Обработка наблюдений и поиск элементов При обработке результатов наблюдений очень часто необходимо установить периодичность изменений блеска, то есть при помощи некоторой искусственной фукции S = S(M), имеющей период, равный среднему периоду звезды, научиться предвидеть моменты максимумов, минимумов или наступление времени некоторых важных процессов (тут М – момент времени). Это делается на основании примерно таких критериев: 1) Периодичность максимумов 2) Периодичность минимумов 3) Стабильность средней кривой изменения блеска как функции от времени. Условие периодичности запишем так: МЕ= M0 + Р ∙ Е точнее, в реальности МЕ (О-С)Е=M0 + Р ∙ Е                                                                                     (4а) где МЕ – момент экстремума звезды, М0– нуль–пункт, начальный момент; Р – период изменения блеска, Е – номер действующего периода Р, или колличество целых значений Р, к-е прошли с момента M0 по M . O-C0– отклонения момента экстремума от того, к-й рассчитан для даного момента E. Перепишем формулу (4) как: 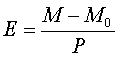                                                                                     (4б) Если в этой формуле через М обозначить не момент экстремума, а произвольный момент времени, Е перестаёт быть целым. Тогда Е можно представить как сумму E + φ, де φ – дробная часть Е в формуле (4б). 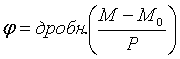                                                                                     (5) Вследствии периодичности функции S(М), её можно представить в виде функции от критерия φ. Соглагласно с теоретическими основами, каждый новый номер Е будет сопровождаться добавлением на графике S (φ) нової хвилі. Таким образом, все пульсации как бы складываются в одну, общую и усреднённую кривую. Рассмотрим случаи, когда моменты M0 + P · E не совпадают с моментом экстремума, то есть еволюционные изменения переменной сопровождаются изменениями её периода. Про эти измения периодов обычно делают выводы по диаграмме O - C. Рассмотрим подробно такой подход к изучению закономерностей блеска переменный звёзд. Итак, (O-C) характеризует степень отклонения момента экстремума O (от англ. – observed)  к расчётному C (англ. – calculated). Когда  можно достатночно уверенно говорить про постоянство периода. Если период звезды изменился, или определён неточно, то . То же самое ми увидим, когда не точно M0. Таким образом, изучая зависимость О-С от E, мы можем найти как изменения периода, так и погрешность в определении M 0. Построим график, отображающий эту зависимость (см. 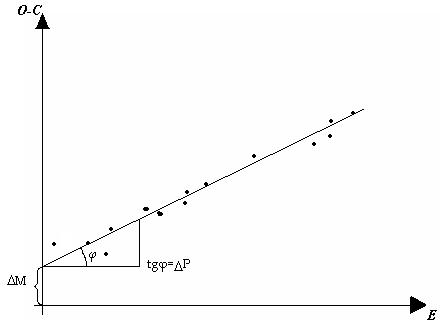Рис.1): Рис.1 Пример линейного роста остатков О-С Если период Р постоянный, график является прямой линией. Понятно, что поправка к величине M 0 определяется точкой пересечения результирующей линии осью О-С. Угловой коэффициент графика определяет погрешность Δ P. Приведём более обстоятельно рассуждения, которые объяснят эти утверждения. Если погрешность определенного периода Р составляет Δ P, то каждый новый период будет увеличивать отклонение О-С на ΔP . Тогда понятно, что О-С ~ ΔP · E (6) Если к тому же момент М0 было вначале определенно неточно, то выражение (6) можно представить: О-С j = M0 + ΔP · Ej                                                                                     (7) Эту формулу (7) будем считать главной при исследовании графиков, которые отображают визуальные наблюдение. Известно, что М0 может быть определен с достаточно низкой точностью. Применение сложных методик практически не повышает точность определения моментов экстремума блеска. Если момент экстремума наблюдался с достаточной частотой, то можно определить Δ(О) с точнистью, которая приблизительно равняется: 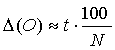 %                                                                                     (8) где t – интервал наблюдений, причем t ≤ Р, N – количество наблюдений ΔМ - погрешность в определении екстремума. Эта формула дает погрешность экстремума на графике, на котором экстремум не является очевидным. Очень часто, аккуратно выполненная серия наблюдений может повысить точность почти в два раза! 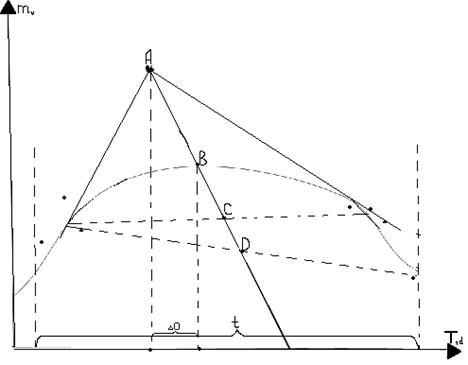Рис. 2 представляет собой иллюстрацию к формуле (8): внутри большого интервала времени t получено 7 точек, что явно не указывают местторасположение максимума функции mv (T) (точка В, определенная методом хорд принадлежит прямой CD, где С и D - средние точки соответствующих хорд). Имея только точки на графике, наблюдатель найдет приблизительное местонахождение максимума, что соответствует точке А. Погрешность такого измерения составит ΔО О. Наведена нами формула (8) позволяет оценить ΔО, полагаясь на многократные измерения этой величины екпериментально. Заметим, что с (8) следует, что для N ЕСТЬ [ ±4%, ±6%]. Из рисунка (1) визначемо ΔМ но ΔР. Чтоб уникнити долговременных и недостаньо точных расчетов, приблизительно проведем черту, что усреднит все наблюдения. Она пересечет ось (O-C) в точке А(О Δ M 0 ). Точность нашего Δ M 0 возьмем такой же, как и в случае N = [ ±4%, ±6%]. Кроме того, погрешность ΔМ0 следует уменьшить у n раз, где n - число пунктов (О-С) - диаграммы. Конечный итог: 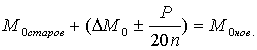                                                                                     (9) Исправив таким образом M0 скорректируем период изменений: имея исправлено М0 и старый период построим новое (О-С) : М = M0нов + Р ∙ Е Оj - Сj = ΔР ∙ Ej - так как ΔМ0 в нашем случае обращено в ноль! Отсюда для одного наблюдения и 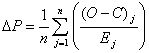                                                                                     (10) Δ(ΔР), погрешность найденого ΔР, составит: 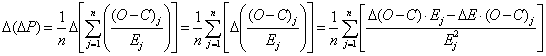                                                                                     (12) Учитывая, что Е - целое число и погрешности в номере пульсации мы не допускаем Δ Е = 0, получим:                                                                                      (13)          формула для погрешности полученного периода. Так как (О-С)= О (Δ С=0 - это теоретически заданная величина), положим и здесь t совпадает с Р. Используя формулу для приближенного подсчета (8): 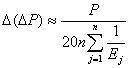                                                                                     (14) С учетом уточнений ΔМ0 и ΔР формула (4) имеет вид : 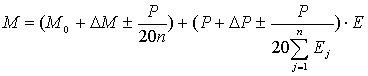, или M нов = М0нов + Рнов ∙ Е с погрешностью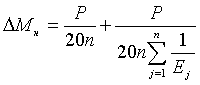                                                                                      (15) Искомые величины и 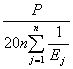- константы. Отсюда погрешность станет линейно зависеть от Е. Формула (15) позволит нам рассчитать с заданной точностью пространство, в котором будут действовать полученные нами элементы. Понятно теперь, что с ростом Е будет расти погрешность (О-С), что и наблюдается в действительности во время исследования любой звезды. Окончательный вид формулы (15): ΔМЕнов = ΔM0 + Δ(ΔР)∙Е                                                                                       (16) Вернуться к оглавлению