1.2 Метод Нейланда-Блажко

 

Как уже было сказано выше, человеческий глаз способен улавливать разницу в блеске двух точечных объектов (звёзд) с точностью около 0,01 m(V). Но количественно оценить столь малую величину ему, наверное, не под силу. Зато, как уже давно доказано на опыте, количественная оценка блеска имеет, всё же, достаточно большую точность – от 0,025 до 0,15 m(V), в зависимости от индивидуальных качеств наблюдателя, характера объекта и других условий. При правильном подборе таких условий можно добиться вполне приличных результатов.

Как же производится визуальная оценка блеска? Существует целый ряд методик. Но самая простая, точная и быстрая – это оценка по методу Нейланда-Блажко.

Этот метод заключается в выборе двух звезд сравнения и звезды, блеск которой измеряется. Желательно, чтобы интервал блеска между звёздами сравнения не превышал 0,4-0,5m(v).

Оценка блеска происходит по алгоритму:

·              Сравнивается блеск яркой звезды и второй по яркости звезды.

·              Сравнивается блеск второй звезды и самой «слабой» из звезд тройки. Оценивание разности блеска проводится визуально по принципу степенной шкалы, которая выглядит примерно так:

0)      ΔS=0 – разница в блеске неощутима или в равной мере сравниваемые звезды кажутся одна ярче другой (следствие атмосферной турбулентности, мерцание).

1)      ΔS=1 – одна из мерцающих звезд кажется ярче несколько чаще, чем другая.

2)      ΔS=2 – разница в блеске ощущается сразу, но она не велика

3)      ΔS=3 – мерцание вообще не играет роли, разница очевидна и значительна.

4)      ΔS=4 – разящая разница.

5)     ΔS=5 – разница в блеске очень и очень внушительна. К примеру, если из пары яркая видна довольно хорошо, слабая может быть на грани видимости.

6)      ΔS=6 – когда слабая на грани видимости, яркая из звезд “слепит” по сравнению со слабой.

7)      ΔS=7 – яркость любой по яркости звезды слишком велика, чтобы сделать точную оценку.

Шкалу сравнения можно изменять, но при этом необходимо сохранить ее главный принцип – оценивание не во сколько раз одна звезда ярче другой, а на сколько! Иначе неизбежны ошибки, а обработке такие наблюдения подлежать не будут.

Получив оценку, запишем ее. Назовем наши звезды сравнения, к примеру, С и D. Переменную звезду обозначим как V. Классическая оценка, выполненная по методу Нейлана–Блажко будет иметь вид С[a]v[b]D:, где a – на сколько C ярче v, а b – на сколько v ярче D. Есть особые случаи, когда к примеру, переменная ярче и С, и D, тогда оценку стоит выполнить в виде: v[x]С[y]D, а М – сумма всех оценок в этом интервале, или, наоборот, блеск изучаемого объекта слабее блеска звёзд сравнения, тогда оценку делаем в виде, например, С[r]D[m]v.

Выберем за нуль – пункт в условной шкале звездных величин (степенной) звезду С. Привяжем к ней блеск v:

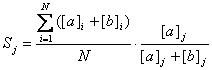
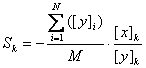                                                 (1)

где   номер оценки, N – число оценок внутри интервала [C;D],  блеск v в системе, где за нуль – пункт выбрана яркость С 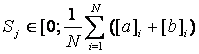, для второй оценки - аналогично.

Метод Нейланда–Блажко предполагает, что зависимость  и () – прямо пропорциональная, тогда очевидно, что

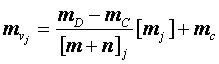                                                                     (2)

Понятно, что в формуле (1) 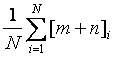 играет роль эквивалента  . Смысл второго слагаемого в формуле (2) в том, что нуль пункт в формуле (1) тут не есть абсолютным и нулевым, а имеет конкретное значение .

Если оценки в интервале [C;D]  не единственны, а есть оценки в интевалах [А;В], [В;С], [D;E], то (1) можно преобразовать к новому значению нуль–пункта (звезда А):

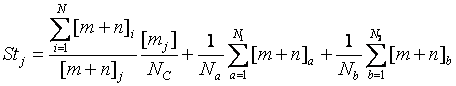                           (3)

где второе слагаемое – средний интервал [А;В],  – число оценок на этом интервале, третье слагаемое – соответственно, средний интервал [В;С],  – число наблюдений на [В;С].

Продолжим далее тему обработки наблюдений.

В данной работе мы постараемся установить периодичность изменения блеска. Это делается на основании трех критериев:

1) Периодичность максимумов

2) Периодичность минимумов

3) Стабильность средней кривой изменения блеска как функции от времени.

Условие периодичности запишем так

                                                                                           (4)

а точнее               (5)                                      где  – момент экстремума звезды, – нуль–пункт, начальный момент, Р – период изменения блеска, Е – номер действующего Р, или количество целых значений Р, прошедших с момента  по . – отклонение момента экстремума от расчетного для данного момента .

Перепишем формулу (4) как:

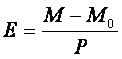                                                                                              (4б)

Если в этой формуле  обозначить не момент экстремума, а произвольное время, Е перестанет быть целым числом. Тогда Е можно представить как сумму + φ, где φ – дробная часть Е в формуле (4б).

Если вдуматься в смысл φ, то можно понять, что это – критерий, согласно которому, вследствие периодичности (t),  может представиться как функция от φ, причем теория указывает на то, что каждый новый номер Е будет сопровождаться добавлением на график (φ) новый волны, совпадающей с предыдущей. Таким образом все пульсации как бы складываются в одну, общую, на которой они теряют индивидуальность, вследствие чего мы можем установить средний вид функции и даже представить ее в виде сложной функции (разложить её в ряд Фурье и т.д.)

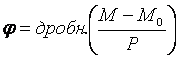                                                                                      (5)

Рассмотрим теперь случаи, когда  не совпадает с моментом экстремума

(O-C) характеризует степень отклонения момента экстремума (O – observed)  от расчетного (C – calculated).

Когда  можно с достаточной степенью уверенности говорить о постоянстве периода.

Если период звезды изменился или неточен, . То же самое будет наблюдаться тогда, когда   недостаточно точно.

Изучая зависимость (О-С)(), мы можем найти и изменение периода, и ошибку в .

Построим график, изображающий эту зависимость.

Если период Р постоянен , то график можно будет представить в виде прямой линии. Очевидно, что то место, где она пересечет ось (О-С) и следует считать поправкой к . Угловой коэффициент графика этой результирующей линии – это .

Данные заключения легко проверяются логически: пусть период Р действительно определен с ошибкой. Назовем её . Из-за этого каждый новый Р будет увеличивать отклонение О от С на . Очевидно, что  (6). Если момент  был изначально неточен, то (6) примет такой вид:

                                                                                       (7)

Эту формулу следует считать основной при исследовании графиков. Известно, что , как любой момент максимума, определяется с очень низкой степенью точности, чаще всего, “на глаз”. Применение сложных методик не только не экономит время, но и не увеличивает точность найденного момента экстремума. Если момент экстремума наблюдался с достаточной частотой, то можно определить Δ(O) с точностью,  равной примерно: 

 

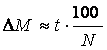                               % ;                                                                      (8)

где N – число наблюдений,  по которым определялся экстремум, а  ΔМ – ошибка в определении экстремума.  ΔМ следует принять как ΔМ ≡ ΔО  в данном случае. Это формула, чаще всего, дает ошибку экстремума для графика, на котором тот не очень очевиден. Часто, аккуратно выполненная серия наблюдений позволяет повысить точность почти в 2 раза!

Эта формула даёт ошибку экстремума на графике, на котором екстремум не очевиднен. Очень часто, аккуратно выполненная серия наблюдений может повысить точность почти в два раза!

 

 

 

 

 

 

 

 

 

 

 

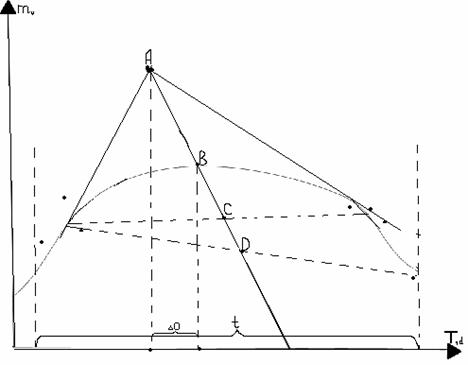
Рис. 1 Еденичный экстремум и графические построения к нему

 

Рис. 1 представляет собой иллюстрацию к формуле (8): внутри большого интервала времени t получено 7 точек, что явно не показывают положение максимума функции m_v(T) (точка В, определённая методом хорд, то есть В принадлежит прямой CD, где С и D – средние точки соответственных хорд). Имея лишь точки на графике, наблюдатель найдёт приблизительное расположение максимума, соответствующее точке А. Погрешность такого измерения составит DО. Приведённая нами формула (8) позволяет оценить DО, полагаясь на многократные измерения этой величины экпериментально.

Заметим, что из (8) следует, что для    Δ [±4%,  ±6%].   Из рисунка  (1) определим   ΔМ  и ΔР.  Чтобы избежать длительных и низкоточных выкладок, примерно построим линию, усредняющую все наблюдения. Она пересекла ось (O-C) в точке А( О, Δ). Точность нашего Δ возьмем такой же, как и в случае для .  В среднем запишем так

                   Δ5% р = Δр.

Кроме того, вероятно,  ошибку Δ следует уменьшить в n раз, где  n  - число пунктов ?? (О-С) – диаграммы. Конечный итог:

 

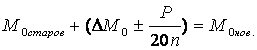                                                                            (9)

        Исправив таким образом  ,  скорректируем сам период изменений: имея исправленное  и старый период построим новое (О-С) и новые ?????элементы:

                               М=

                               О-  -  т.к.  Δ  в нашем случае обнулилось!

Отсюда 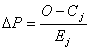      для одного наблюдения  и

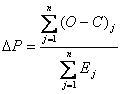                                                                                                        (10)

ошибка найденного ΔР    Δ(ΔР) составит:

                                                                                    (11)

Так  как  Е – величина  целая – то  второе  слагаемое  не  имеет  приращения, т.е. равно 0. Отсюда легко найти    Δ(ΔР):

               ???????

Подставляя  (10)  в  (12), получаем:

                                                                  (13) 

-  формула для ошибки найденного периода.

Применяя еще и формулу для приближенного счета (9), получаем

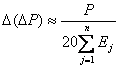                                                                                                         (14)

В итоге, применяя формулы  (9)  и (13;14)   получаем:

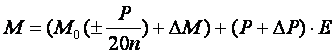,   или

с ошибкой 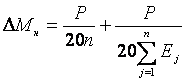                                                                             (15)

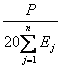Величины   и  следует определить, как константы. Тогда ошибка представится зависимостью от Е, линейной.

Формула (15) позволит определить интервал (О-С), который можно считать как то пространство возможных отклонений (О-С) в дальнейшем от новых элементов, точки, попавшие в которое не считаются такими, что являются предпосыльными для пересчёта периода.

Конечный вид формулы (15):

                                                                                                        (16)

а – начальная ошибка момента M, k – коэффициент увеличения ошибки.

Рассмотрим пример применения рассмотренного нами математического алгоритма.

Пусть мы имеем 20 отметок на диаграмме (О-С), , задаём . Тогда, согласно (15):

,

откуда, корректируя Р , получаем

.

То есть, после того, как мы получаем 20 оценок (О-С), мы можем с достаточной точностью предвидеть около 4000 моментов звезды.

Также видем, что при увеличении колличества точек на (О-С) диаграмме, качество определения элементов пульсации почти неулучшается, главный вклад тут вносит , то есть желательно наблюдать как можно более “длинные” интервалы времени.